Question 1.
If f (x) = 2x and g (x) = \(\frac{x^2}{2}\) + 1, then’which of the following can be a discontinuous function
(a) f(x) + g(x)
(b) f(x) – g(x)
(c) f(x).g(x)
(d) \(\frac{g(x)}{f(x)}\)

Answer

Answer: (d) \(\frac{g(x)}{f(x)}\)

---

Question 2.
The function f(x) = \(\frac{4-x^2}{4x-x^3}\) is
(a) discontinuous at only one point at x = 0
(b) discontinuous at exactly two points
(c) discontinuous at exactly three points
(d) None of these

Answer

Answer: (a) discontinuous at only one point at x = 0

---

Question 3.
The set of points where the function f given by f (x) =| 2x – 1| sin x is differentiable is
(a) R
(b) R = {\(\frac{1}{2}\)}
(c) (0, ∞)
(d) None of these

Answer

Answer: (b) R = {\(\frac{1}{2}\)}

---

Question 4.
The function f(x) = cot x is discontinuous on the set
(a) {x = nπ, n ∈ Z}
(b) {x = 2nπ, n ∈ Z}
(c) {x = (2n + 1) \(\frac{π}{2}\) n ∈ Z}
(d) {x – \(\frac{nπ}{2}\) n ∈ Z}

Answer

Answer: (a) {x = nπ, n ∈ Z}

---

Question 5.
The function f(x) = e^|x| is
(a) continuous everywhere but not differentiable at x = 0
(b) continuous and differentiable everywhere
(c) not continuous at x = 0
(d) None of these

Answer

Answer: (a) continuous everywhere but not differentiable at x = 0

---

Question 6.
If f(x) = x² sin\(\frac{1}{x}\), where x ≠ 0, then the value of the function f(x) at x = 0, so that the function is continuous at x = 0 is
(a) 0
(b) -1
(c) 1
(d) None of these

Answer

Answer: (a) 0

---

Question 7.
If f(x) =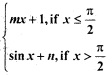is continuous at x = \(\frac{π}{2}\), then
(a) m = 1, n = 0
(b) m = \(\frac{nπ}{2}\) + 1
(c) n = \(\frac{mπ}{2}\)
(d) m = n = \(\frac{π}{2}\)

Answer

Answer: (c) n = \(\frac{mπ}{2}\)

---

Question 8.
If y = log(\(\frac{1-x^2}{1+x^2}\)), then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{4x^3}{1-x^4}\)
(b) \(\frac{-4x}{1-x^4}\)
(c) \(\frac{1}{4-x^4}\)
(d) \(\frac{-4x^3}{1-x^4}\)

Answer

Answer: (b) \(\frac{-4x}{1-x^4}\)

---

Question 9.
Let f(x) = |sin x| Then
(a) f is everywhere differentiable
(b) f is everywhere continuous but not differentiable at x = nπ, n ∈ Z
(c) f is everywhere continuous but no differentiable at x = (2n + 1) \(\frac{π}{2}\) n ∈ Z
(d) None of these

Answer

Answer: (b) f is everywhere continuous but not differentiable at x = nπ, n ∈ Z

---

Question 10.
If y = \(\sqrt{sin x+y}\) then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{cosx}{2y-1}\)
(b) \(\frac{cosx}{1-2y}\)
(c) \(\frac{sinx}{1-xy}\)
(d) \(\frac{sinx}{2y-1}\)

Answer

Answer: (a) \(\frac{cosx}{2y-1}\)

---

Question 11.
The derivative of cos^-1 (2x² – 1) w.r.t cos^-1 x is
(a) 2
(b) \(\frac{-1}{2\sqrt{1-x^2}}\)
(c) \(\frac{2}{x}\)
(d) 1 – x²

Answer

Answer: (a) 2

---

Question 12.
If x = t², y = t³, then \(\frac{d^2y}{dx^2}\)
(a) \(\frac{3}{2}\)
(b) \(\frac{3}{4t}\)
(c) \(\frac{3}{2t}\)
(d) \(\frac{3}{4t}\)

Answer

Answer: (b) \(\frac{3}{4t}\)

---

Question 13.
The value of c in Rolle’s theorem for the function f(x) = x³ – 3x in the interval [o, √3] is
(a) 1
(b) -1
(c) \(\frac{3}{2}\)
(d) \(\frac{1}{3}\)

Answer

Answer: (a) 1

---

Question 14.
For the function f(x) = x + \(\frac{1}{x}\), x ∈ [1, 3] the value of c for mean value theorem is
(a) 1
(b) √3
(c) 2
(d) None of these

Answer

Answer: (b) √3

---

Question 15.
Let f be defined on [-5, 5] as
f(x) = {\(_{-x, if x is irrational}^{x, if x is rational}\) Then f(x) is
(a) continuous at every x except x = 0
(b) discontinuous at everyx except x = 0
(c) continuous everywhere
(d) discontinuous everywhere

Answer

Answer: (b) discontinuous at everyx except x = 0

---

Question 16.
Let function f (x) =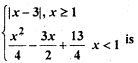
(a) continuous at x = 1
(b) differentiable at x = 1
(c) continuous at x = -3
(d) All of these

Answer

Answer: (d) All of these

---

Question 17.
If f(x) = \(\frac{\sqrt{4+x}-2}{x}\) x ≠ 0 be continuous at x = 0, then f(o) =
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{4}\)
(c) 2
(d) \(\frac{3}{2}\)

Answer

Answer: (b) \(\frac{1}{4}\)

---

Question 18.
let f(2) = 4 then f”(2) = 4 then \(_{x→2}^{lim}\) \(\frac{xf(2)-2f(x)}{x-2}\) is given by
(a) 2
(b) -2
(c) -4
(d) 3

Answer

Answer: (c) -4

---

Question 19.
It is given that f'(a) exists, then \(_{x→2}^{lim}\) [/latex] \(\frac{xf(a)-af(x)}{(x-a)}\) is equal to
(a) f(a) – af'(a)
(b) f'(a)
(c) -f’(a)
(d) f (a) + af'(a)

Answer

Answer: (a) f(a) – af'(a)

---

Question 20.
If f(x) = \(\sqrt{25-x^2}\), then \(_{x→2}^{lim}\)\(\frac{f(x)-f(1)}{x-1}\) is equal to
(a) \(\frac{1}{24}\)
(b) \(\frac{1}{5}\)
(c) –\(\sqrt{24}\)
(d) \(\frac{1}{\sqrt{24}}\)

Answer

Answer: (d) \(\frac{1}{\sqrt{24}}\)

---

Question 21.
If y = ax² + b, then \(\frac{dy}{dx}\) at x = 2 is equal to ax
(a) 4a
(b) 3a
(c) 2a
(d) None of these

Answer

Answer: (a) 4a

---

Question 22.
If x sin (a + y) = sin y, then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{sin^2(a+y)}{sin a}\)
(b) \(\frac{sin a}{sin^2(a+y)}\)
(c) \(\frac{sin(a+y)}{sin a}\)
(d) \(\frac{sin a}{sin(a+y)}\)

Answer

Answer: (a) \(\frac{sin^2(a+y)}{sin a}\)

---

Question 23.
If x \(\sqrt{1+y}+y\sqrt{1+x}\) = 0, then \(\frac{dy}{dx}\) =
(a) \(\frac{x+1}{x}\)
(b) \(\frac{1}{1+x}\)
(c) \(\frac{-1}{(1+x)^2}\)
(d) \(\frac{x}{1+x}\)

Answer

Answer: (c) \(\frac{-1}{(1+x)^2}\)

---

Question 24.
If y = x tan y, then \(\frac{dy}{dx}\) =
(a) \(\frac{tan x}{x-x^2-y^2}\)
(b) \(\frac{y}{x-x^2-y^2}\)
(c) \(\frac{tan y}{y-x}\)
(d) \(\frac{tan x}{x-y^2}\)

Answer

Answer: (b) \(\frac{y}{x-x^2-y^2}\)

---

Question 25.
If y = (1 + x) (1 + x²) (1 + x⁴) …….. (1 + x²ⁿ), then the value of \(\frac{dy}{dx}\) at x = 0 is
(a) 0
(b) -1
(c) 1
(d) None of these

Answer

Answer: (c) 1

---

Question 26.
If f(x) = \(\frac{5x}{(1-x)^{2/3}}\) + cos² (2x + 1), then f'(0) =
(a) 5 + 2 sin 2
(b) 5 + 2 cos 2
(c) 5 – 2 sin 2
(d) 5 – 2 cos 2

Answer

Answer: (c) 5 – 2 sin 2

---

Question 27.
If sec(\(\frac{x^2-2x}{x^2+1}\)) – y then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{y*2}{x^2}\)
(b) \(\frac{2y\sqrt{y^2-1}(x^2+x-1)}{(x^2+1)^2}\)
(c) \(\frac{(x^2+x-1)}{y\sqrt{y^2-1}}\)
(d) \(\frac{x^2-y^2}{x^2+y^2}\)

Answer

Answer: (b) \(\frac{2y\sqrt{y^2-1}(x^2+x-1)}{(x^2+1)^2}\)

---

Question 28.
If f(x) = \(\sqrt{1+cos^2(x^2)}\), then the value of f’ (\(\frac{√π}{2}\)) is
(a) \(\frac{√π}{6}\)
(b) –\(\frac{√π}{6}\)
(c) \(\frac{1}{√6}\)
(d) \(\frac{π}{√6}\)

Answer

Answer: (b) –\(\frac{√π}{6}\)

---

Question 29.
Differential coefficient of \(\sqrt{sec√x}\) is
(a) \(\frac{1}{4√x}\) = sec √x sin √x
(b) \(\frac{1}{4√x}\) = (sec√x)^3/2 sin√x
(c) \(\frac{1}{2}\) √x sec√x sin √x.
(d) \(\frac{1}{2}\)√x (sec√x)^3/2 sin√x

Answer

Answer: (b) \(\frac{1}{4√x}\) = (sec√x)^3/2 sin√x

---

Question 30.
Let f(x)={\(_{1-cos x, for x ≤ 0}^{sin x, for x > 0}\) and g (x) = e^x. Then the value of (g o f)’ (0) is
(a) 1
(b) -1
(c) 0
(d) None of these

Answer

Answer: (c) 0

---

Question 31.
If x^myⁿ = (x + y)^m+n, then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{x+y}{xy}\)
(b) xy
(c) \(\frac{x}{y}\)
(d) \(\frac{y}{x}\)

Answer

Answer: (d) \(\frac{y}{x}\)

---

Question 32.
If \(\sqrt{(x+y)}\) + \(\sqrt{(y-x)}\) = a, then \(\frac{dy}{dx}\)

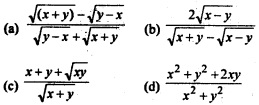
Answer

Answer: (a) \(\frac{\sqrt{(x+y)}-\sqrt{(y-x)}}{\sqrt{y-x}+\sqrt{x+y}}\)

---

Question 33.
If ax² + 2hxy + by² = 1, then \(\frac{dy}{dx}\)equals
(a) \(\frac{hx+by}{ax+by}\)
(b) \(\frac{ax+by}{hx+by}\)
(c) \(\frac{ax+hy}{hx+hy}\)
(d) \(\frac{-(ax+hy)}{hx+by}\)

Answer

Answer: (d) \(\frac{-(ax+hy)}{hx+by}\)

---

Question 34.
If sec (\(\frac{x-y}{x+y}\)) = a then \(\frac{dy}{dx}\) is
(a) –\(\frac{y}{x}\)
(b) \(\frac{x}{y}\)
(c) –\(\frac{x}{y}\)
(d) \(\frac{y}{x}\)

Answer

Answer: (d) \(\frac{y}{x}\)

---

Question 35.
If y = tan^-1(\(\frac{sinx+cosx}{cox-sinx}\)) then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{1}{2}\)
(b) \(\frac{π}{4}\)
(c) 0
(d) 1

Answer

Answer: (d) 1

---

Question 36.
If y = tan^-1(\(\frac{√x-x}{1+x^{3/2}}\)), then y'(1) is equal to
(a) 0
(b) (\(\frac{√x-x}{1+x^{3/2}}\))
(c) -1
(d) –\(\frac{1}{4}\)

Answer

Answer: (d) –\(\frac{1}{4}\)

---

Question 37.
The differential coefficient of tan^-1(\(\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}\)) is
(a) \(\sqrt{1-x^2}\)
(b) \(\frac{1}{\sqrt{1-x^2}}\)
(c) \(\frac{1}{2\sqrt{1-x^2}}\)
(d) x

Answer

Answer: (c) \(\frac{1}{2\sqrt{1-x^2}}\)

---

Question 38.
\(\frac{d}{dx}\)[tan^-1(\(\frac{a-x}{1+ax}\))] is equal to

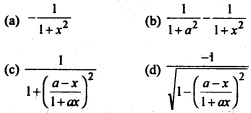
Answer

Answer: (a) –\(\frac{1}{1+x^2}\)

---

Question 39.
\(\frac{d}{dx}\)(x\(\sqrt{a^2-x^2}+a^2 sin^{-1}(\frac{x}{a})\)) is equal to
(a) \(\sqrt{a^2-x^2}\)
(b) 2\(\sqrt{a^2-x^2}\)
(c) \(\frac{1}{\sqrt{a^2-x^2}}\)
(d) None of these

Answer

Answer: (b) 2\(\sqrt{a^2-x^2}\)

---

Question 40.
If f(x) = tan^-1(\(\sqrt{\frac{1+sinx}{1-sinx}}\)), 0 ≤ x ≤ \(\frac{π}{2}\), then f'(\(\frac{π}{6}\)) is
(a) –\(\frac{1}{4}\)
(b) –\(\frac{1}{2}\)
(c) \(\frac{1}{4}\)
(d) \(\frac{1}{2}\)

Answer

Answer: (d) \(\frac{1}{2}\)

---

Question 41.
If y = sin^-1(\(\frac{√x-1}{√x+1}\)) + sec^-1(\(\frac{√x+1}{√x-1}\)), x > 0, then \(\frac{dy}{dx}\) is equal to
(a) 1
(b) 0
(c) \(\frac{π}{2}\)
(d) None of these

Answer

Answer: (b) 0

---

Question 42.
If x = exp {tan^-1(\(\frac{y-x^2}{x^2}\))}, then \(\frac{dy}{dx}\) equals
(a) 2x [1 + tan (log x)] + x sec² (log x)
(b) x [1 + tan (log x)] + sec² (log x)
(c) 2x [1 + tan (logx)] + x² sec² (log x)
(d) 2x [1 + tan (log x)] + sec² (log x)

Answer

Answer: (a) 2x [1 + tan (log x)] + x sec² (log x)

---

Question 43.
If y = e^3x+n, then the value of \(\frac{dy}{dx}\)|_x=0 is
(a) 1
(b) 0
(c) -1
(d) 3e⁷

Answer

Answer: (d) 3e⁷

---

Question 44.
Let f (x) = e^x, g (x) = sin^-1 x and h (x) = f |g(x)|, then \(\frac{h'(x)}{h(x)}\) is equal to
(a) e^sin-1x
(b) \(\frac{1}{\sqrt{1-x^2}}\)
(c) sin^-1x
(d) \(\frac{1}{(1-x^2)}\)

Answer

Answer: (b) \(\frac{1}{\sqrt{1-x^2}}\)

---

Question 45.
If y = ae^x+ be^-x + c Where a, b, c are parameters, they y’ is equal to
(a) ae^x – be^-x
(b) ae^x + be^-x
(c) -(ae^x + be^-x)
(d) ae^x – be^x

Answer

Answer: (a) ae^x – be^-x

---

Question 46.
If sin y + e^{-xcos y} = e, then \(\frac{dy}{dx}\) at (1, π) is equal to
(a) sin y
(b) -x cos y
(c) e
(d) sin y – x cos y

Answer

Answer: (c) e

---

Question 47.
Derivative of the function f (x) = log₅ (Iog,x), x > 7 is
(a) \(\frac{1}{x(log5)(log7)(log7-x)}\)
(b) \(\frac{1}{x(log5)(log7)}\)
(c) \(\frac{1}{x(logx)}\)
(d) None of these

Answer

Answer: (a) \(\frac{1}{x(log5)(log7)(log7-x)}\)

---

Question 48.
If y = log₁₀x + log y, then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{y}{y-1}\)
(b) \(\frac{y}{x}\)
(c) \(\frac{log_{10}e}{x}\)(\(\frac{y}{y-1}\))
(d) None of these

Answer

Answer: (c) \(\frac{log_{10}e}{x}\)(\(\frac{y}{y-1}\))

---

Question 49.
If y = log [e^x(\(\frac{x-1}{x-2}\))\(^{1/2}\)], then \(\frac{dy}{dx}\) is equal to
(a) 7
(b) \(\frac{3}{x-2}\)
(c) \(\frac{3}{(x-1)}\)
(d) None of these

Answer

Answer: (d) None of these

---

Question 50.
If y = e^{\(\frac{1}{2}\) log(1+tan²x)}, then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{1}{2}\) sec² x
(b) sec² x
(c) sec x tan x
(d) e^{\(\frac{1}{2}\) log(1+tan²x)}

Answer

Answer: (c) sec x tan x

---

Question 51.
If y = 2^x3^2x-1 then \(\frac{dy}{dx}\) is equal to dx
(a) (log 2) (log 3)
(b) (log lg)
(c) (log 18²) y²
(d) y (log 18)

Answer

Answer: (d) y (log 18)

---

Question 52.
If x^x = y^y, then \(\frac{dy}{dx}\) is equal to
(a) –\(\frac{y}{x}\)
(b) –\(\frac{x}{y}\)
(c) 1 + log (\(\frac{x}{y}\) )
(d) \(\frac{1+logx}{1+logy}\)

Answer

Answer: (d) \(\frac{1+logx}{1+logy}\)

---

Question 53.
If y = (tan x)^{sin x}, then \(\frac{dy}{dx}\) is equal to
(a) sec x + cos x
(b) sec x+ log tan x
(c) (tan x)^{sin x}
(d) None of these

Answer

Answer: (d) None of these

---

Question 54.
If x^y = e^x-y then \(\frac{dy}{dx}\) is
(a) \(\frac{1+x}{1+log x}\)
(b) \(\frac{1-log x}{1+log y}\)
(c) not defined
(d) \(\frac{-y}{(1+log x)^2}\)

Answer

Answer: (d) \(\frac{-y}{(1+log x)^2}\)

---

Question 55.
The derivative of y = (1 – x) (2 – x)…. (n – x) at x = 1 is equal to
(a) 0
(b) (-1) (n – 1)!
(c) n ! – 1
(d) (-1)^n-1 (n – 1)!

Answer

Answer: (b) (-1) (n – 1)!

---

Question 56.
If f(x) = cos x, cos 2 x, cos 4 x, cos 8 x, cos 16 x, then the value of'(\(\frac{π}{4}\)) is
(a) 1
(b) √2
(c) \(\frac{1}{√2}\)
(d) 0

Answer

Answer: (b) (-1) (n – 1)!

---

Question 57.
x^y. y^x = 16, then the value of \(\frac{dy}{dx}\) at (2, 2) is
(a) -1
(b) 0
(c) -1
(d) None of these

Answer

Answer: (a) -1

---

Question 58.
If y = e^{x+ex+ex+….to∞} find \(\frac{dy}{dx}\) =
(a) \(\frac{y^2}{1-y}\)
(b) \(\frac{y^2}{y-1}\)
(c) \(\frac{y}{y-1}\)
(d) \(\frac{-y}{y-1}\)

Answer

Answer: (c) \(\frac{y}{y-1}\)

---

Question 59.
If x = \(\frac{1-t^2}{1+t^2}\) and y = \(\frac{2t}{1+t^2}\) then \(\frac{dy}{dx}\) is equal to dx
(a) –\(\frac{y}{x}\)
(b) \(\frac{y}{x}\)
(c) –\(\frac{x}{y}\)
(d) \(\frac{x}{y}\)

Answer

Answer: (c) –\(\frac{x}{y}\)

---

Question 60.
If x = a cos⁴ θ, y = a sin⁴ θ. then \(\frac{dy}{dx}\) at θ = \(\frac{3π}{4}\) is
(a) -1
(b) 1
(c) -a²
(d) a²

Answer

Answer: (a) -1

---

Question 61.
If x = sin^-1 (3t – 4t³) and y = cos^-1 (\(\sqrt{1-t^2}\)) then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{1}{2}\)
(b) \(\frac{2}{5}\)
(c) \(\frac{3}{2}\)
(d) \(\frac{1}{3}\)

Answer

Answer: (d) \(\frac{1}{3}\)

---

Question 62.
Let y = t¹⁰ + 1 and x = t⁸ + 1, then \(\frac{d^2y}{dx^2}\), is equal to
(a) \(\frac{d^2y}{dx^2}\)
(b) 20t⁸
(c) \(\frac{5}{16t^6}\)
(d) None of these

Answer

Answer: (d) \(\frac{1}{3}\)

---

Question 63.
The derivative of e^x3 with respect to log x is
(a) e^e3
(b) 3x²2e^x3
(c) 3x³e^x3
(d) 3x²e^x3+ 3x²

Answer

Answer: (c) 3x³e^x3

---

Question 64.
If x = e^t sin t, y = e^tcos t, t is a parameter, then \(\frac{dy}{dx}\) at (1, 1) is equal to
(a) –\(\frac{1}{2}\)
(b) –\(\frac{1}{4}\)
(c) 0
(d) \(\frac{1}{2}\)

Answer

Answer: (c) 0

---

Question 65.
The derivative of sin^-1 (\(\frac{2x}{1+x^2}\)) with respect to cos^-1 (\(\frac{1-x^2}{1+x^2}\)) is
(a) -1
(b) 1
(c) 2
(d) 4

Answer

Answer: (b) 1

---