Question 1.
Feasible region in the set of points which satisfy
(a) The objective functions
(b) Some the given constraints
(c) All of the given constraints
(d) None of these

Answer

Answer: (c) All of the given constraints

---

Question 2.
Of all the points of the feasible region for maximum or minimum of objective function the points
(a) Inside the feasible region
(b) At the boundary line of the feasible region
(c) Vertex point of the boundary of the feasible region
(d) None of these

Answer

Answer: (c) Vertex point of the boundary of the feasible region

---

Question 3.
Objective function of a linear programming problem is
(a) a constraint
(b) function to be obtimized
(c) A relation between the variables
(d) None of these

Answer

Answer: (b) function to be obtimized

---

Question 4.
A set of values of decision variables which satisfies the linear constraints and nn-negativity conditions of a L.P.P. is called its
(a) Unbounded solution
(b) Optimum solution
(c) Feasible solution
(d) None of these

Answer

Answer: (c) Feasible solution

---

Question 5.
The maximum value of the object function Z = 5x + 10 y subject to the constraints x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x ≥ 0, y ≥ 0 is
(a) 300
(b) 600
(c) 400
(d) 800

Answer

Answer: (b) 600

---

Question 6.
The maximum value of Z = 4x + 2y subject to the constraints 2x + 3y ≤ 18, x + y ≥ 10, x, y ≤ 0 is
(a) 36
(b) 40
(c) 30
(d) None of these

Answer

Answer: (d) None of these

---

Question 7.
In equation 3x – y ≥ 3 and 4x – 4y > 4
(a) Have solution for positive x and y
(b) Have no solution for positive x and y
(c) Have solution for all x
(d) Have solution for all y

Answer

Answer: (a) Have solution for positive x and y

---

Question 8.
The maximum value of Z = 3x + 4y subjected to contraints x + y ≤ 40, x + 2y ≤ 60, x ≥ 0 and y ≥ 0 is
(a) 120
(b) 140
(c) 100
(d) 160

Answer

Answer: (b) 140

---

Question 9.
Maximize Z = 11 x + 8y subject to x ≤ 4, y ≤ 6, x + y ≤ 6, x ≥ 0, y ≥ 0.
(a) 44 at (4, 2)
(b) 60 at (4, 2)
(c) 62 at (4, 0)
(d) 48 at (4, 2)

Answer

Answer: (b) 60 at (4, 2)

---

Question 10.
Maximize Z = 3x + 5y, subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0
(a) 20 at (1, 0)
(b) 30 at (0, 6)
(c) 37 at (4, 5)
(d) 33 at (6, 3)

Answer

Answer: (c) 37 at (4, 5)

---

Question 11.
Maximize Z = 4x + 6y, subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0
(a) 16 at (4, 0)
(b) 24 at (0, 4)
(c) 24 at (6, 0)
(d) 36 at (0, 6)

Answer

Answer: (d) 36 at (0, 6)

---

Question 12.
Maximize Z = 7x + 11y, subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0
(a) 59 at (\(\frac{9}{2}\), \(\frac{5}{2}\))
(b) 42 at (6, 0)
(c) 49 at (7, 0)
(d) 57.2 at (0, 5.2)

Answer

Answer: (a) 59 at (\(\frac{9}{2}\), \(\frac{5}{2}\))

---

Question 13.
Maximize Z = 6x + 4y, subject to x ≤ 2, x + y ≤ 3, -2x + y ≤ 1, x ≥ 0, y ≥ 0
(a) 12 at (2, 0)
(b) \(\frac{140}{3}\) at (\(\frac{2}{3}\), \(\frac{1}{3}\))
(c) 16 at (2, 1)
(d) 4 at (0, 1)

Answer

Answer: (c) 16 at (2, 1)

---

Question 14.
Maximize Z = 10 x₁ + 25 x₂, subject to 0 ≤ x₁ ≤ 3, 0 ≤ x₂ ≤ 3, x₁ + x₂ ≤ 5
(a) 80 at (3, 2)
(b) 75 at (0, 3)
(c) 30 at (3, 0)
(d) 95 at (2, 3)

Answer

Answer: (d) 95 at (2, 3)

---

Question 15.
Z = 20x₁ + 20₂, subject to x₁ ≥ 0, x₂ ≥ 0, x₁ + 2x₂ ≥ 8, 3x₁ + 2x₂ ≥ 15, 5x₁ + 2x₂ ≥ 20. The minimum value of Z occurs at
(a) (8, 0)
(b) (\(\frac{5}{2}\), \(\frac{15}{4}\))
(c) (\(\frac{7}{2}\), \(\frac{9}{4}\))
(d) (0, 10)

Answer

Answer: (c) (\(\frac{7}{2}\), \(\frac{9}{4}\))

---

Question 16.
Z = 6x + 21 y, subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at
(a) (4, 0)
(b) (28, 8)
(c) (2, \(\frac{7}{2}\))
(d) (0, 3)

Answer

Answer: (c) (2, \(\frac{7}{2}\))

---

Question 17.
The corner point of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20, 40), (60, 20), (60, 0). The objective function is Z = 4x + 3y.
Compare the quantity in Column A and Column B

Column A	Column B
Maximum of Z	325

(a) The quantity in column A is greater
(b) The quantity in column B is greater
(c) The two quantities are equal
(d) The relationship cannot be determined On the basis of the information supplied

Answer

Answer: (b) The quantity in column B is greater

---

Question 18.
The feasible region for a LPP is shown shaded in the figure. Let Z = 3x – 4y be the objective function. Minimum of Z occurs at

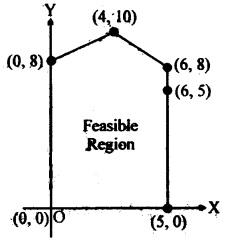
(a) (0, 0)
(b) (0, 8)
(c) (5, 0)
(d) (4, 10)

Answer

Answer: (b) (0, 8)

---

Question 19.
Refer to Question 18 maximum of Z occurs at
(a) (5, 0)
(b) (6, 5)
(c) (6, 8)
(d) (4, 10)

Answer

Answer: (a) (5, 0)

---

Question 20.
Refer to Question 18 (Maximum value of Z+ Minimum value of Z) is equal to
(a) 13
(b) 1
(c) -13
(d) -17

Answer

Answer: (d) -17

---