Question 1.
If f(x₁) = f (x₂) ⇒ x₁ = x₂ ∀ x₁ x₂ ∈ A then the function f: A → B is
(a) one-one
(b) one-one onto
(c) onto
(d) many one

Answer

Answer: (a) one-one

---

Question 2.
What type of a relation is R = {(1, 3), (4, 2), (2, 4), (2, 3), (3, 1)} on the set A – {1, 2, 3, 4}
(a) Reflexive
(b) Transitive
(c) Symmetric
(d) None of these

Answer

Answer: (d) None of these

---

Question 3.
If F : R → R such that f(x) = 5x + 4 then which of the following is equal to f^-1(x).
(a) \(\frac{x-5}{4}\)
(b) \(\frac{x-y}{5}\)
(c) \(\frac{x-4}{5}\)
(d) \(\frac{x}{4}\) -5

Answer

Answer: (c) \(\frac{x-4}{5}\)

---

Question 4.
If an operation is defined by a* b = a² + b², then (1 * 2) * 6 is
(a) 12
(b) 28
(c) 61
(d) None of these

Answer

Answer: (c) 61

---

Question 5.
Consider the binary operation * on a defined by x * y = 1 + 12x + xy, ∀ x, y ∈ Q, then 2 * 3 equals
(a) 31
(b) 40
(c) 43
(d) None of these

Answer

Answer: (a) 31

---

Question 6.
The range of the function f(x) = \(\sqrt{(x-1)(3-x)}\) is
(a) [1, 3]
(b) [0, 1]
(c) [-2, 2]
(d) None of these

Answer

Answer: (a) [1, 3]

---

Question 7.
If f: R → R defined by f(x) = 2x + 3 then f^-1(x) =
(a) 2x – 3
(b) \(\frac{x-3}{2}\)
(c) \(\frac{x+3}{2}\)
(d) None of these

Answer

Answer: (b) \(\frac{x-3}{2}\)

---

Question 8.
The function f(x) = log (x² + \(\sqrt{x^2+1}\) ) is
(a) even function
(b) odd function
(c) Both
(d) None of these

Answer

Answer: (a) even function

---

Question 9.
Let E = {1, 2, 3, 4} and F = {1, 2} Then, the number of onto functions from E to F is
(a) 14
(b) 16
(c) 12
(d) 8

Answer

Answer: (a) 14

---

Question 10.
If A, B and C are three sets such that A ∩ B = A ∩ C and A ∪ B = A ∪ C. then
(a) A = B
(b) A = C
(c) B = C
(d) A ∩ B = d

Answer

Answer: (c) B = C

---

Question 11.
Let A = {1, 2}, how many binary operations can be defined on this set?
(a) 8
(b) 10
(c) 16
(d) 20

Answer

Answer: (c) 16

---

Question 12.
Let A = {1, 2, 3, 4,…. n} How many bijective function f : A → B can be defined?
(a) \(\frac{1}{2}\)n

(d) n

Answer

Answer: (c) [n

---

Question 13.
If A = (1, 2, 3}, B = {6, 7, 8} is a function such that f(x) = x + 5 then what type of a function is f?
(a) Many-one onto
(b) Constant function
(c) one-one onto
(d) into

Answer

Answer: (c) one-one onto

---

Question 14.
Let function R → R is defined as f(x) = 2x³ – 1, then ‘f’ is
(a) 2x³ + 1
(b) (2x)³ + 1
(c) (1 – 2x)³
(d) (\(\frac{1+x}{2}\))^1/3

Answer

Answer: (d) (\(\frac{1+x}{2}\))^1/3

---

Question 15.
Let the functioin ‘f’ be defined by f (x) = 5x² + 2 ∀ x ∈ R, then ‘f’ is
(a) onto function
(b) one-one, onto function
(c) one-one, into function
(d) many-one into function

Answer

Answer: (d) many-one into function

---

Question 16.
A relation R in human being defined as, R = {{a, b) : a, b ∈ human beings : a loves A} is-
(a) reflexive
(b) symmetric and transitive
(c) equivalence
(d) None of these

Answer

Answer: (c) equivalence

---

Question 17.
If f(x) + 2f (1 – x) = x² + 2 ∀ x ∈ R, then f(x) =
(a) x² – 2
(b) 1
(c) \(\frac{1}{3}\) (x – 2)²
(d) None of these

Answer

Answer: (c) \(\frac{1}{3}\) (x – 2)²

---

Question 18.
The period of sin² θ is
(a) π²
(b) π
(c) 2π
(d) \(\frac{π}{2}\)

Answer

Answer: (b) π

---

Question 19.
The domain of sin-1 (log (x/3)] is. .
(a) [1, 9]
(b) [-1, 9]
(c) [-9, 1]
(d) [-9, -1]

Answer

Answer: (a) [1, 9]

---

Question 20.
f(x) = \(\frac{log_2(x+3)}{x^2+3x+2}\) is the domain of
(a) R – {-1, -2}
(b) (- 2, ∞) .
(c) R- {- 1,-2, -3}
(d) (-3, + ∞) – {-1, -2}

Answer

Answer: (d) (-3, + ∞) – {-1, -2}

---

Question 21.
If the function f(x) = x³ + e^x/2 and g (x) = fⁿ(x), then the value of g'(1) is
(a) 1
(b) 2
(c) 3
(d) 4

Answer

Answer: (b) 2

---

Question 22.
What type of relation is ‘less than’ in the set of real numbers?
(a) only symmetric
(b) only transitive
(c) only reflexive
(d) equivalence

Answer

Answer: (b) only transitive

---

Question 23.
If A = [1, 2, 3}, B = {5, 6, 7} and f: A → B is a function such that f(x) = x + 4 then what type of function is f?
(a) into
(b) one-one onto
(c) many-onto
(d) constant function

Answer

Answer: (b) one-one onto

---

Question 24.
f: A → B will be an into function if
(a) range (f) ⊂ B
(b) f(a) = B
(c) B ⊂ f(a)
(d) f(b) ⊂ A

Answer

Answer: (a) range (f) ⊂ B

---

Question 25.
If f : R → R such that f(x) = 3x then what type of a function is f?
(a) one-one onto
(b) many one onto
(c) one-one into
(d) many-one into

Answer

Answer: (c) one-one into

---

Question 26.
If f: R → R such that f(x) = 3x – 4 then which of the following is f^-1(x)?
(a) \(\frac{1}{3}\) (x + 4)
(b) \(\frac{1}{3}\) (x – 4)
(c) 3x – 4
(d) undefined

Answer

Answer: (a) \(\frac{1}{3}\) (x + 4)

---

Question 27.
A = {1, 2, 3} which of the following function f: A → A does not have an inverse function
(a) {(1, 1), (2, 2), (3, 3)}
(b) {(1, 2), (2, 1), (3, 1)}
(c) {(1, 3), (3, 2), (2, 1)}
(d) {(1, 2), (2, 3), (3, 1)

Answer

Answer: (b) {(1, 2), (2, 1), (3, 1)}

---

Question 28.
Let T be the set of all triangles in the Euclidean plane, and let a relation R on T be defined as aRb if a congruent to b ∀ a, b ∈ T. Then R is
(a) reflexive but-not transitive
(b) transitive but not symmetric
(c) equivalence
(d) None of these

Answer

Answer: (c) equivalence

---

Question 29.
Consider the non-empty set consisting of children is a family and a relation R defined as aRb If a is brother of b. Then R is
(a) symmetric but not transitive
(b) transitive but not symmetric
(c) neither symmetric nor transitive
(d) both symmetric and transitive

Answer

Answer: (b) transitive but not symmetric

---

Question 30.
The maximum number of equivalence relations on the set A = {1, 2, 3} are
(a) 1
(b) 2
(c) 3
(d) 5

Answer

Answer: (d) 5

---

Question 31.
If a relation R on the set {1, 2, 3} be defined by R = {(1, 2)}, then R is
(a) reflexive
(b) transitive
(c) symmetric
(d) None of these

Answer

Answer: (b) transitive

---

Question 32.
Let us define a relation R in R as aRb if a ≥ b. Then R is
(a) an equivalence relation
(b) reflexive, transitive but not symmetric
(c) neither transitive nor reflexive but symmetric
(d) symmetric, transitive but not reflexive

Answer

Answer: (b) reflexive, transitive but not symmetric

---

Question 33.
Let A = {1, 2, 3} and consider the relation R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3), (1, 3)}. Then R is
(a) reflexive but not symmetric
(b) reflexive-but not transitive.
(c) symmetric and transitive
(d) neither symmetric, nor transitive

Answer

Answer: (a) reflexive but not symmetric

---

Question 34.
The identity element for the binary operation * defined on Q ~ {0} as
a * b = \(\frac{ab}{2}\) ∀ a, b ∈ Q ~ {0} is
(a) 1
(b) 0
(c) 2
(d) None of these

Answer

Answer: (c) 2

---

Question 35.
If the set A contains 5 elements and the set B contains 6 elements, then the number of one-one and onto mappings from A to B is
(a) 720
(b) 120
(c) 0
(d) None of these

Answer

Answer: (c) 0

---

Question 36.
Let A = {1, 2,3,…. n} and B = { a, b}. Then the number of surjections from A into B is
(a) ⁿP₂
(b) 2ⁿ – 2
(c) 2ⁿ – 1
(d) None of these

Answer

Answer: (b) 2ⁿ – 2

---

Question 37.
Let f : R → R be defined by f (x) = \(\frac{1}{x}\) ∀ x ∈ R. Then f is
(a) one-one
(b) onto
(c) bijective
(d) f is not defined

Answer

Answer: (d) f is not defined

---

Question 38.
Let f: R → R. be defined by f (x) = 3x² – 5 and g : R → R by g (x) = \(\frac{x}{x^2+1}\). Then g o f is

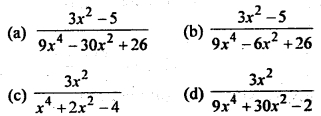
Answer

Answer: (a)

---

Question 39.
Which of the following functions from Z into Z are bijective?
(a) f(x) = x³
(b) f(x) = x + 2
(c) f(x) = 2x + 1
(d) f{x) = x² + 1

Answer

Answer: (b) f(x) = x + 2

---

Question 40.
Let f: R → R be the function defined by f(x) = x³ + 5. Then f^-1 (x) is
(a) (x + 5)^1/3
(b) (x -5)^1/3
(c) (5 – x)^1/3
(d) 5 – x

Answer

Answer: (b) (x -5)^1/3

---

Question 41.
Let f: A → B and g : B → C be the bijective functions. Then (g o f)^-1 is,
(a) f^-1 o g^-1
(b) f o g
(c ) g^-1 o f^-1
(d) g o f

Answer

Answer: (a) f^-1 o g^-1

---

Question 42.
Let f: R – {\(\frac{3}{5}\)} → R be defined by f(x) = \(\frac{3x+2}{5x-3}\) then
(a) f^-1(x) = f(x)
(b) f^-1(x) = -f(x)
(c ) (f o f)x = -x
(d ) f^-1(x) = \(\frac{1}{19}\) f(x)

Answer

Answer: (a) f^-1(x) = f(x)

---

Question 43.
Let f: [0, 1| → [0, 1| be defined by

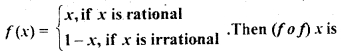
(a) Constant
(b) 1 + x
(c) x
(d) None of these

Answer

Answer: (c) x

---

Question 44.
Let f: |2, ∞) → R be the function defined by f(x) – x² – 4x + 5, then the range of f is
(a) R
(b) [1, ∞)
(c) [4, ∞)
(d) [5, ∞)

Answer

Answer: (b) [1, ∞)

---

Question 45.
Let f: N → R be the function defined by f(x) = \(\frac{2x-1}{2}\) and g: Q → R be another function defined by g (x) = x + 2. Then (g 0 f) \(\frac{3}{2}\) is
(a) 1
(b) 0
(c) \(\frac{7}{2}\)
(d) None of these

Answer

Answer: (d) None of these

---

Question 46.
Let f: R → R be defined by

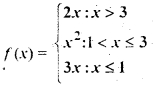
then f(- 1) + f (2) + f (4) is
(a) 9
(b) 14
(c) 5
(d) None of these

Answer

Answer: (a) 9

---

Question 47.
Let f : R → R be given by f (,v) = tan x. Then f^-1(1) is
(a) \(\frac{π}{4}\)
(b) {nπ + \(\frac{π}{4}\) : n ∈ Z}
(c) does not exist
(d) None of these

Answer

Answer: (b) {nπ + \(\frac{π}{4}\) : n ∈ Z}

---

Question 48.
The relation R is defined on the set of natural numbers as {(a, b): a = 2b}. Then, R^-1 is given by
(a) {(2, 1), (4, 2), (6, 3),….}
(b) {(1, 2), (2, 4), (3, 6),….}
(c) R^-1 is not defined
(d) None of these

Answer

Answer: (b) {(1, 2), (2, 4), (3, 6),….}

---

Question 49.
The relation R = {(1,1), (2, 2), (3, 3), (1, 2), (2, 3), (1, 3)} on set A = {1, 2, 3} is
(a) Reflexive but not symmetric
(b) Reflexive but not transitive
(c) Symmetric and transitive
(d) Neither symmetric nor transitive

Answer

Answer: (a) Reflexive but not symmetric

---

Question 50.
Let P = {(x, y) | x² + y² = 1, x, y ∈ R]. Then, P is
(a) Reflexive
(b) Symmetric
(c) Transitive
(d) Anti-symmetric

Answer

Answer: (b) Symmetric

---

Question 51.
Let R be an equivalence relation on a finite set A having n elements. Then, the number of ordered pairs in R is
(a) Less than n
(b) Greater than or equal to n
(c) Less than or equal to n
(d) None of these

Answer

Answer: (b) Greater than or equal to n

---

Question 52.
For real numbers x and y, we write xRy ⇔ x – y + √2 is an irrational number. Then, the relational R is
(a) Reflexive
(b) Symmetric
(c) Transitive
(d) None of these

Answer

Answer: (a) Reflexive

---

Question 53.
Let R be a relation on the set N be defined by {(x, y) | x, y ∈ N, 2x + y = 41}. Then R is
(a) Reflexive
(b) Symmetric
(c) Transitive
(d) None of these

Answer

Answer: (d) None of these

---

Question 54.
Which one of the following relations on R is an equivalence relation?
(a) aR₁b ⇔ |a| = |b|
(b) aR₂b ⇔ a ≥ b
(c) aR₃b ⇔ a divides b
(d) aR₄b ⇔ a < b

Answer

Answer: (a) aR₁b ⇔ |a| = |b|

---

Question 55.
Let R be a relation on the set N of natural numbers denoted by nRm ⇔ n is a factor of m (i.e. n | m). Then, R is
(a) Reflexive and symmetric
(b) Transitive and symmetric
(c) Equivalence
(d) Reflexive, transitive but not symmetric

Answer

Answer: (d) Reflexive, transitive but not symmetric

---